Earlier today I set you these problems from the Mathigon puzzle advent calendar. Here they are again with solutions.
1. The knights are drawing in.

Solution

2. The missing numbers round.

Solution
Each number is the sum of the previous two numbers. 1 + 3 = 4, 3 + 4 = 7, and so on. It’s just like the Fibonacci sequence, which obeys the same rule but begins 0, 1.
3. Square are you?

Solution

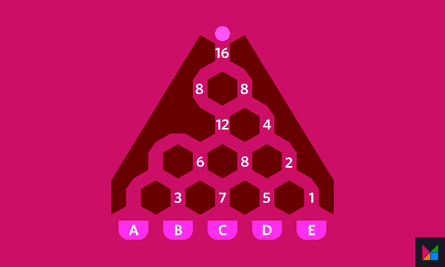
4. Hexa-going, hexa-going, hexagon.

Solution 3/16
5. Satsuma segment

Solution 25/16
This one requires a bit more workings. You will need to use Pythagoras’s theorem for right angled triangles too: the square of the hypotenuse is equal to the sum of the squares on the other two sides. The first thing is to extend the semicircle to show the full circle, and draw in the triangle below. The circle meets the left side of the square in the middle. The left corner of the triangle is a right angle because every point on a circle subtends a right angle with the diameter.
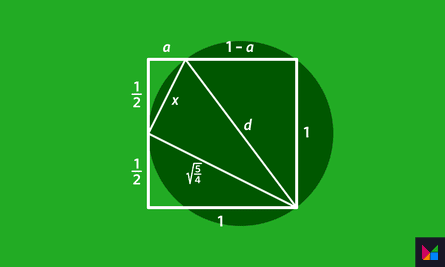
Thus d2 = a2 + (1/2)2 + 5/4
and d2 = (1 – a)2 + 1
Thus a2 + 6/4 = 1 – 2a + a2 + 1
2a = 2 – 6/4 = 1/2
a = 1/4, and when you plug in this value d = 25/16
I hope you enjoyed today’s puzzles. I’ll be back in two weeks…on Christmas Day!
Thanks to Mathigon, which belongs to international edtech firm Amplify. Mathigon is one of the most engaging and creative maths resources on the web, and is free. Check it out!
I’ve been setting a puzzle here on alternate Mondays since 2015. I’m always on the look-out for great puzzles. If you would like to suggest one, email me.





