Earlier today I set you these problems from the book Lateral Solutions to Mathematical Problems by Des MacHale. Here they are again with answers.
1. Three cloves on an orange
Given three points on the surface of a sphere, what is the probability there is a hemisphere on which they all lie?
Answer 100 per cent
Don’t do any caclulations. Think of it like this: put two random points on the surface of the sphere (i.e. insert two cloves randomly on an orange). Now cut the sphere (the orange) in half with the cut going through these two points (the cloves). You now have two hemispheres, both of which include the two points. The third random point (or clove) will be on one of these hemispheres.
2. A big number
If you multiply all the prime numbers less than one million together, what is the final digit of your answer?
[A prime number is a number that is divisible only by itself and 1, such as 2, 3, 5, 7, 11, 13, and so on.]
Answer: The number will end in 0.
Again, don’t even think of multiplying them all up. The number is 2 x 3 x 5 x 7 x ….
Since 2 x 5 = 10, we can rewrite this as 10 x 3 x 7 x ….
Any whole number that is a multiple of 10 ends in 0.
3. The three threes
Can you make 20 using three threes and any mathematical operations you like?
[i.e you need to find an expression that includes 3, 3 and 3, and no other digits, but may include any other mathematical symbol, such as +, -, x, ÷, (, ), √, ., etc. An example might be 3√3/3, although this would be wrong since it does not equal 20.]
Answer
The trick is to use a decimal point. Here’s one way:
20 = (3 + 3)/.3
4. Square are you?
How can you cut this figure into four pieces which can be reassembled to form a square?
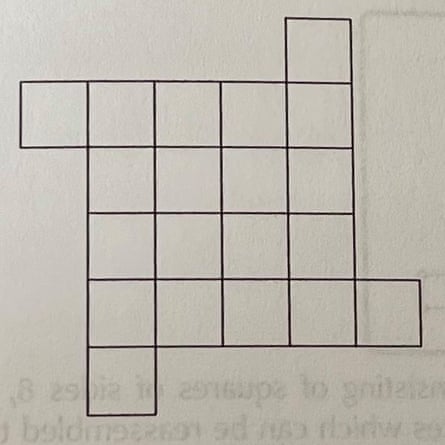
Solution
There are 20 small squares in the shape. So if they are to be put together to form a large square, this large square must have a side of √20. Let’s try to find a line in the diagram that is √20 long.
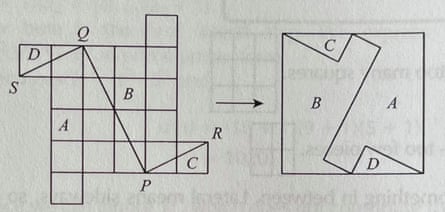
Pythagoras’s Theorem for right-angled triangles states that the square of the hypotenuse is equal to the sum of the squares on the other two sides. Since 22 + 42 = 20 = (√20)2 we know that the hypotenuse of a right angled triangle with short sides 2 and 4, will provide us with our required length. In the image below, therefore, PQ has length √20. Since we are making a square, another good bet would be that the cut at P and Q heads off at 90 degrees. And voila.
5. Roamin’ numerals
Make the equation valid by moving exactly two matchsticks
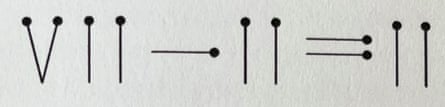
Answer Here’s one way.
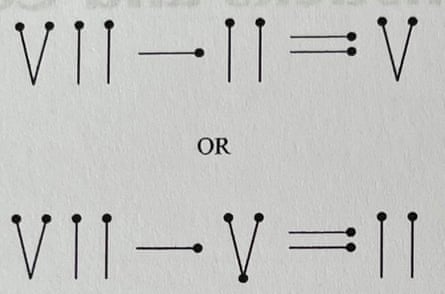
And here’s another:
If you found any other, please let me know below the line!
Thanks to Des MacHale for today’s puzzles, which are all taken from his excellent new book Lateral Solutions to Mathematical Problems.
I’ve been setting a puzzle here on alternate Mondays since 2015. I’m always on the look-out for great puzzles. If you would like to suggest one, email me.





