Sometimes it pays to approach a problem sideways. Each of today’s puzzles requires some lateral thinking, in that the first step of the solution is perhaps not the obvious one.
1. Three cloves on an orange
Given three points on the surface of a sphere, what is the probability there is a hemisphere on which they all lie?
2. A big number
If you multiply all the prime numbers less than one million together, what is the final digit of your answer?
[A prime number is a number that is divisible only by itself and 1, such as 2, 3, 5, 7, 11, 13, and so on.]
3. The three threes
Can you make 20 using three threes and any mathematical operations you like?
[i.e you need to find an expression that includes 3, 3 and 3, and no other digits, but may include any other mathematical symbol, such as +, -, x, ÷, (, ), √, ., etc. An example might be 3√3/3, although this would be wrong since it does not equal 20.]
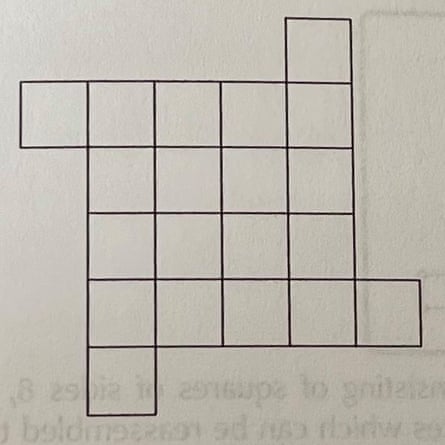
4. Square are you?
How can you cut this figure into four pieces which can be reassembled to form a square?
5. Roamin’ numerals
Make the equation valid by moving exactly two matchsticks
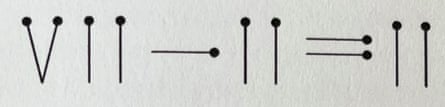
Please NO SPOILERS. I’ll be back at 5pm UK. Instead discuss your favourite examples of lateral-thinking.
UPDATE: To read the solutions click here.
All of today’s puzzle come from Des MacHale’s brilliant new book Lateral Solutions to Mathematical Problems, in which he presents more than a 100 problems from across the mathematical landscape whose solutions benefit from out-of-the-box thinking.
MacHale, emeritus professor at University College, Cork, is well known to readers of this column as an encyclopedia of mathematical humour. Hs latest book replaces the the “haha” with the “aha!”
(Hopefully, with not too much aaaaaaaargh!)
I’ve been setting a puzzle here on alternate Mondays since 2015. I’m always on the look-out for great puzzles. If you would like to suggest one, email me.





